THE RECTANGLE SEARCH

Original Problem: With the length and width of a rectangle each
a different single digit number, prove...

sometimes the perimeter number
is more than the area number

sometimes the perimeter number
equals the area number

sometimes the perimeter number
is less than the area number

Use diagrams to prove your points.

1. Problem Statement

This problem is called The Rectangle Search. The problem is to find three different rectangles each with a single digit number for the length and the width that are different from each other and one that is the same. One must have it's perimeter less than the area and one vice versa. The last one has to have equal area and perimeter.

2. Process

I tried to solve the problem by drawing different rectangles and figuring out their perimeters and area. At first I just guessed different lengths and widths and found part of the answer. This is the guess and check method. I couldn't guess a rectangle with equal perimeter and area so, I had to go through every possible rectangle and check the perimeter and area. This is called an exhaustive search.

My First Guesses

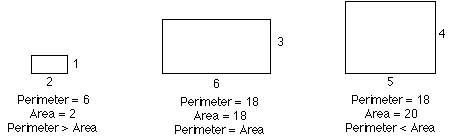
I started out by drawing all of the rectangles in this picture.

Doing this I found out some things, first I found a rectangle whose perimeter was bigger than its area. I also found a rectangle whose perimeter was less than its area. I also found out that it didn't matter which way I put the length and width on one of the pictures. The area and the perimeter came out the same either way.

Making A List

I kept trying but I couldn't find a rectangle where they were equal. After trying many rectangles and not finding one with equal area and perimeter I found out that I was trying some rectangles more than once. So I needed to make a list that would keep track of what I had tried and what I hadn't.

To do this I made a table that listed rectangle lengths, widths, areas and perimeters. First I listed all the rectangles with length equal to 1. Since the sides had to be different there were 8 of these. Then I listed the rectangles with length equal to 2. I didn't have to list the one whose width was 1 because it was just like the rectangle with length 1 and width 2. This meant there were only 7 of these rectangles. Then I listed 6 rectangles with length equal to 3, 5 rectangles with length 4 and so on. My table looked like this:

Length
Width
Perimeter
Area
1
2
6
2
1
3
8
3
1
4
10
4
1
5
12
5
1
6
14
6
1
7
16
7
1
8
18
8
1
9
20
9
2
3
10
6
2
4
12
8
2
5
14
10
2
6
16
12
2
7
18
14
2
8
20
16
2
9
22
18
3
4
14
12
3
5
16
15
3
6
18
18
3
7
20
21
3
8
22
24
3
9
24
27
4
5
18
20
4
6
20
24
4
7
22
28
4
8
24
32
4
9
26
36
5
6
22
30
5
7
24
35
5
8
26
40
5
9
28
45
6
7
26
42
6
8
28
48
6
9
30
54
7
8
30
56
7
9
32
63
8
9
34
72

My Answer

Once I had my table I could see that there were lots of choices except for the rectangle that had equal perimeter and area. These are the rectangles I picked to solve the problems.


3. Evaluation

This problem was easy. I liked this problem because I'm good with areas and perimeters. Finding the first rectangle was the hardest part of the problem. I didn't learn anything. I'm proud that I got a solution.

Back to PGFPP...